Biographies of famous mathematicians

With the intention of building interest on students of 2 ESO and 3 ESO for Mathematics, they have been requested to do an investigation on biographies of famous mathematicians. Biographies help young people to understand the complex studies of Mathematics, putting a human face on a field that students tent to see as very abstract. Allowing them as well to discover some of the major results in Mathematics and their applications. Hereby some of the most outstanding results of their investigations. Congratulations to all!

 

Carl Friedrich Gauss

By Daniel Abreu García y Saúl Díaz Navarro, students from 3ºESO-B

Hello, readers from LA TIZA MENSAJERA! Today, we are going to talk about one of the greatest mathematicians that ever existed in the world: Carl Friedrich Gauss.

He was born on 30 april of 1777 in Brunswick (Germany), and he died on 23 February of 1855 in Göttingen (Germany), aged 77. During his mathematical career he was resident in “Reino Hanover» where he spent the most time of his life.

Gauss was an amazing german mathematician and physicist, who made incredible contributions to the history of maths and science. From child, he was considered a prodigy and he made some significant discoveries as a teenager. He came from a farmer family and their fathers didn’t have much culture. But his love for the maths was very strong.

When he was nine years old, in an arithmetic class, he resolved in a very fast way the addition of the first 100 numbers (1+2+3…+100). With a formula that surprised even his teacher. (Solution= 101/2 x 100 =5050).

At age 19, he discovered a beautiful construction of a 17-sided regular figure – a heptadecagon – using only a ruler and compass, something that for 2,000 years had been thought impossible.

At that age, perhaps to keep up with his many advances, he began to keep a mathematical journal. The entries start in 1796 and the latest is dated on July 9, 1814.

Disquisitiones arithmeticae is a book on number theory written by himself in 1798 when he was 21 years old and first published in 1801 in Leipzig.

In 1791, Duke Ferdinand offered to pay for the university studies of Gauss, who was then, 14 years old. In November 1806, his protector, Duke Ferdinand, was mortally  wounded in a battle against Napoleon’s army. But the mysterious Monsieur Le Blanc used his influence to make sure nothing bad happened to the bright young Gauss.

He unveiled the Gaussian function (or Gaussian bell), after a problem with Ceres, which is one of the pillars of statistics. It is the visual representation of the frequency of a given data group.

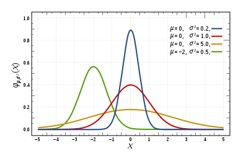
He also established “Gauss’s law” in physics: which establishes that the flow of certain fields through a closed surface is proportional to the magnitude of the sources of said field that are inside the same surface.

Without a doubt, Gauss has been one of the best mathematicians that has ever existed and that will exist. His discoveries have left a valuable legacy that is still talked about and used today.

“Mathematics is the queen of science and arithmetic is the queen of mathematics. She often deigns to render a service to astronomy and other natural sciences, but in all relationships, she is entitled to the front row”, Carl Friedrich Gauss.

 

Blaise Pascal, what a genius

By Agoney Dorta Pérez, student from 3ºESO-B

In the 17^th century, science wasn’t still completely developed, but, indeed, there were lots of smart people with purposes of studying and investigating. The human beings curiosity explains this, and Pascal was very curious.

He was a mathematician, philosopher and french physicist. His contributions to science were the result of his love for it. He also got interested in philosophy, most oriented to christian religion. He talked about human condition and its almost insignificant existence. Let’s learn about him by talking about his contributions to science and inventions, which, indeed, are still used today.

Pascal Theorem:

It was published in 1639 in the book called Essai pour les Coniques (Essay on Conics). The theorem explains that if we extend the lines of a hexagon, then the pairs of the sides create a straight line.

In that year, he moved to Rouan with his father as he was hired as a Tax Commissioner. But thanks to his knowledge regarding Girard Desargues ideas, he was capable of writing this book.

Existence of Void:

In 1647, he proved for the first time the existence of void by several tests with the barometer and mercury, demonstrating the theory of Torricelli. In 1645 he started working with physics and doing his first experiments with void. This is one of his discoveries.

Atmospheric Pressure:

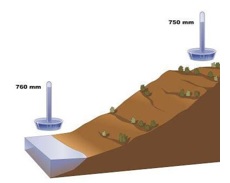
This was a topic that had been discussed before, but Pascal was who made the decisive test. He filled two different barometers with mercury. Let’s give them B1 for the first one and B2 for the second one. B2 was left on the base of a mountain, and B1 was raised to the top of it. Pascal realized as he was going up, that the level of Mercury descended.

In this way, he proved that for more height, less pressure.

Principle of Pascal:

It was formulated in 1648 and it explains that when an isolated fluid goes through pressure in one of its points, that pressure will be  exerted in all the points of the fluid. An example is a mat: if we prick it in three different points, the air will go out of them in the same pressure.

Triangle of Pascal:

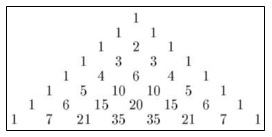
It was formulated in 1653 and set the bases for the development of the theory of probability.

This numeric pattern was already studied before, but Pascal was who gave it the right interpretation.

The triangle starts at the top, with the number 1, and continues with this number to the sides of the triangle. The sum of the numbers above give the ones below. As the numbers are infinite, the triangle is too, and it will grow to the sides infinitely.

This discovery is interesant, not only for all it uses in science, but also for the period in which it was created. In 1645 he started a mundane period recommended by doctors in Paris, but, still, he didn’t shut down his scientific work completely. That would happen some years after.

Theorem of Probability:

It appears in 1654. Pascal used his triangle to give the theorem a form, as some probabilities can be calculated considering what happened before. In this way, Pascal, in a card game that was interrupted, was able to divide up the money fairly. He used his theory and deduced the next plays considering the ones that already had happened.

In his mundane period, he used to play cards, and this discovery was a need in his plays, as if a game wasn’t finished, he had the way to divide up the money wagered.

Pascaline:

It appears in 1645 and could be considered as the first calculator ever built. It was created to make his father’s job easier, when he worked as a tax commissioner. In this way, he could sum and subtract just by putting the number on the different wheels and round them. In the next video you’ll find an example of the Pascaline.

Game of Roulette:

This game is said to be invented in China and brought to Europe by traders. But there is another theory much more convincing that says that Pascal invented it. Indeed, roulette means wheel in french, and in his resting period he used to go to the casino.

Even Pascal created a roulette which contained 36 numbers, without 0, because he wanted a machine in continuous movement.

What more evidence is needed to prove it?

Hydraulic Press:

It is a system that proves the Principle of Pascal: it is a liquid in a closed recipient with two pistons that can move. In that way, when we apply pressure to one of them, the other one is going to go through the same pressure.

Collective Carriages:

In 1662 he suggested the idea of a collective service of carriages, in the one fixed timetables, routes and prices were established.

Some months later, he will pass away from stomach cancer.Today, he is still recognised for all his work, and he will be never forgotten.

These are his most important works, but not the only ones. During all his years of life, he experimented with his own theories to prove other theories and more.

 

Biography of Archimedes

By Omar Dorta Hernández y Lucas Pardo Parra, students from 3ºESO-C

Probably born in 287 BC, Archimedes was the most famous and prestigious mathematician and inventor of his time. His writings, of which a dozen have been preserved, are a proof of his diverse scientific knowledge. His studies were perfected in Alexandria, a great center of Hellenistic culture, where Archimedes went around 243 BC as a disciple of the astronomer and mathematician Conon of Samos, for whom he always had respect and admiration.

Some years later, he returned to Syracuse, where he dedicated himself fully to scientific work. Nevertheless, around the year 212 BC, while the Roman Empire sacked Syracuse (led by Marcus Claudius Marcellus), the old mathematician found himself meditating on his geometry problems. This passion of Archimedes for mathematics caused his death because, when a soldier broke into the room he was in, Archimedes begged him to let him solve the problem he was doing before getting killed. The soldier, contravening the orders of his general, didn’t listen to him and killed him. It is said that this passion was also the one that made him forget to eat and also that he used to amuse himself by drawing geometric drawings in the ashes.

Archimedes contributed to science and mathematics in many different ways: he made discoveries in branches of physics such as statics and hydrostatics, contributed to mathematics by calculating π (pi) using the exhaustive method and by calculating the area under a parabola, discovered a way to calculate the density of a solid by submerging it in water, studied and explained the principle of the lever and even invented the spiral that bears his name.

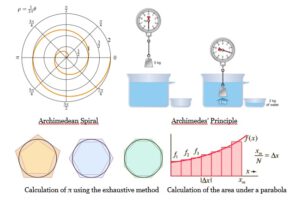
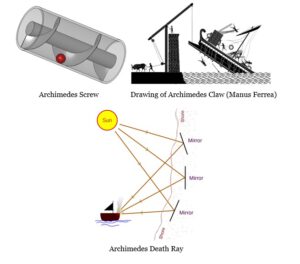
He also created different inventions that were very advanced for his time, such as the Archimedes’ Screw, which let him transport water from a place to a higher one using a crank; the “Manus Ferrea”, a kind of crane that allowed the bow of enemy ships to be raised and suddenly released to sink them; or his famous Death Ray, a construction of bronze mirrors arranged in the shape of a parabola that concentrated sunlight and burned enemy ships (although it is not proven that it actually existed). In fact, some ancient historians claim that when the enemy Roman armies approached the walls of Syracuse with their ships, they trembled in fear if they saw any strange construction in the walls, because they knew that it was the work of Archimedes and it could be dangerous for them. Archimedes ended his life being one of the most remarkable mathematicians and inventors in history, laying the foundations of science for discoveries of future generations.

Isaac Newton

By Arianna González Lobato and María Soler Lozano students from  2° ESO A

Isaac Newton  was born on December 25, 1642 in a manger in the English town of Woolsthorpe.  He was an english physicist, matematician, astronomer and one of the most influential scientists of all time . He was a professor at the University of Cambridge, representative of the British Parliament, inspector and director of the London Mint, president of the Royal Society, and was even awarded the title of Sir. Isaac Newton was buried with all honors in the famous Westminster Abbey.

Despite the limited publicity that his discoveries had at present, Isaac Newton became the undisputed protagonist of the Scientific Revolution of the 16th century.

Newton was one of the inventors of calculus, built the first reflecting telescope, calculated the speed of the sound, studied the motion of fluids, and developed a theory of coloured based on how a prism split sunlight into a renbow-coloured spectrum. Among his many achievements, classical mechanics, the binomial theorem and the discovery of the integral calculus stand out, which contributed to an almost absolute renovation of mathematics. However, physics was the terrain where Newton stood out from the rest of the thinkers of the time.

A brilliant mind that, at times, suffered serious psychic crises, causing long periods of isolation. Depression, hypochondria, paranoia, insomnia, behavioral changes … Symptoms that many related to mercury poisoning, after conducting their alchemical experiments. Despite being a man of science, Isaac Newton always displayed an exacerbated passion for religion. Among his views he defended Arianism, a non-Trinitarian Christian belief, and issues related to esotericism.

His place in history came with the publication of his most important work: «Mathematical principles of natural philosophy.» In it, Isaac Newton formulated the three fundamental laws of motion: the law of inertia, the law of dynamics, and the law of action and reaction. The combination of all of them gave rise to a fourth principle, the most significant: the law of gravity. Legend has it that Newton discovered this last point after seeing an apple fall from a tree, giving rise to the universal law of gravitation that still prevails today.

Until his death on March 20, 1727, due to a kidney disease, Newton not only dedicated his life to research.

As a kid

As a child, he already demonstrated the talent that he has for science. This passion fueled his career at the University of Cambridge, where his research turned to physics and mathematics, giving rise to a multitude of theories and writings with only 29 years of age.

In maths

Although Newton is best known for discoveries in physics, we must not forget his math skills. Under Isaac Barrow’s supervision during his studies at Trinity College, Cambridge, Newton entrusted him with a manuscript that he wrote on various mathematical conclusions.

Integral and differential calculus involves other mathematical calculations such as:

Newton’s document, denominated analysis, describes integral and differential calculus. Newton called it the method of fluxions.

Isaac Newton is also known by what is called Newton’s binomial, that is, the Formula (A + b) n possible independent of the value n.

History goes that when Isaac Barrow retired, he recommended hiring Newton at Trinity College in Cambridge as the new math teacher. Newton and the university agreed.

 

Friedrich Bernhard Riemann

By Nestor Padilla González and Adrián Díaz, students from 2ºESO-A

George Friedrich Bernhard Riemann, was a well-known german mathematician that lived in the 19th century. He was born the 17th of September of 1826 in Bredelenz in the Hannover Kingdom, what’s now Germany. He died on the 20th of July of 1866, at the age of 39 in Selasca in the Italian Kingdom. He dead because of tuberculosis, that is an illness caused by Mycobacterium Tuberculosis, that is a   bacteria that usually affects the lungs.

This illness is transferred by the air and it can affect the order main organs like the heart or the kidneys. Riemann was a Luteran, that is someone who’s religion is the lutheranism. This religion is derived from christianism that is based with the theology of Martin Luthero, who was a doctrinal reformer, theologian and German friar.

This brilliant mathematician studied in Gotinga’s University in Germany and also in the Berlin Humboldt University in Germany. Bernhard’s father was called as he, his Mother was Charlotte Ebell and he had five siblings, Clara, Ida, Helene, Marie and Wilhelm Riemann. He also had a daughter called Ida Schilling with his wife Elise Koch.

Riemann was an amazing kid, he had a wonderful intelligence, but not all was good for Bernhard at school. He was shy and he had problems socializing with other children. He was so smart that his level exceeded the teachers level and he could correct what they said. When he passed to the University he wanted to study mathematics, that was his dream, but his family didn’t have money so he started to study agriculture. When his father saw how big Riemann’s talent was, he worked the hardest he could so finally he reached the money for his son to leave and study at a good university.

Something that not everyone knows about him, is that before leaving his house to study, he passed through the military and he was one of the people in charge of taking care of the King in the Berlin’s war. Finally he came out unharmed and he could continue his path.

Now starting to speak about his life after he studied, he formed part of many mathematics associations and societies. He was part of Gotinga’s Science Academy, Prussian Science Academy, Bavieras Science Academy and also of the Royal Society.

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point that varies smoothly from point to point. This gives, in particular, local notions of angle, length of curves, surface area and volume.

The  surface of Bernhard is a complex variety of dimension one. Consequently, the actual underlying variety will be dimension 2.

The Riemann integration  is the simplest form of integration, yet it lays down the foundation of all other types of integrals.

Generalizations of Riemann varieties Pseudo-Marmannian variety, in which the requirement that the metric tensioner give rise to a positive definite quadratic shape on each point in the tangent space is removed, and replaced by the weaker requirement that the metric tensioner is simply not degenerated.

And for finishing the metric tensioner is a range 2 tensioner that is used to define metric concepts such as distance, angle, and volume in a locally euclidean space.