Problemas matemáticos de Olimpiadas

Problema 1. Desarrollado por Marco Alonso Hernández y Javier Hernández Armas (1ºESO-A).

En un campamento de verano se organizó una competición con 10 problemas. Cada respuesta correcta valía 5 puntos y por cada incorrecta se restaron 3 puntos. No hubo preguntas sin contestar. Pedro tuvo 34 puntos, David 10 y Nerea 2. ¿Cuántas respuestas incorrectas tuvieron entre los 3?

Pedro tuvo 8 bien, que son 40 puntos y luego 2 mal, que da un resultado de menos 6 puntos; así que 40-6 da un igual de 34 puntos. David tuvo 5 bien, que da un igual de 25 ,puntos y luego otras 5 mal, que son 15 puntos menos; así que haríamos una resta de 25-15, que da un igual de 10 puntos. Y por último Nerea tuvo 4 preguntas acertadas que da un igual 20 puntos, y tuvo 6 mal; así que da un resultado de 18 puntos menos. 20-18 da un igual de 2 puntos. Entre los tres tuvieron 13 preguntas mal.

Problema 2. Desarrollado por Ian Rodríguez Torres y Brais Santillán Méndez (1ºESO-D).

Silvia dibuja hormigas de la siguiente forma: una hormiga roja, otra verde, otra amarilla, otra negra, roja, verde, amarilla, negra, roja, verde, amarilla, negra… ¿De qué color es la hormiga 3.452?

Este es un problema sutil. Sin embargo se puede resolver de muchas y diversas maneras. Pero Ian y Brais hemos decidido hacerlo de esta manera:
Como podemos observar cada 4 hormigas, se repite de nuevo la secuencia de colores, por lo que si dividimos 3.452/4, nos dice que en la secuencia número 863 la hormiga 3.452 es de color negro. Ya que si nos fijamos 3.453 ya seria roja empezando la secuencia 864.

Problemas 1 y 2. Desarrollado por Camila Pacheco Herrera y Daniela Montoya Díaz (1ºESO-B).

En un campamento de verano se organizó una competición con 10 problemas. Cada respuesta correcta valía 5 puntos y por cada incorrecta se restaban 3 puntos. No hubo preguntas sin contestar. Pedro tuvo 34 puntos, David 10 y Nerea 2. ¿Cuántas respuestas incorrectas tuvieron entre los 3?

En total, los tres fallaron 13 preguntas. Aquí la explicación: Primero para hacerlo más sencillo, vamos a tratar el problema “como si fuera una persona”. Entonces han contestado a 30 preguntas (10 preguntas por persona). Sabemos también que fueron 46 los puntos en total (34+10+2=46)→ Los datos que tenemos hasta ahora son: -que se realizaron 30 preguntas; -tuvieron 46 puntos en total; -por cada acierto te dan 5 puntos y por cada fallo te quitan 3 (llamaremos a los aciertos “x” y a los errores “y”). Entonces, con estos datos, sabemos que los aciertos más los errores de los niños fueron 30, que expresado con una fórmula sería: x+y=30. También podemos afirmar que las preguntas acertadas (+5) menos las preguntas falladas (-3), les otorgaron un total de 46 puntos, que expresado con una fórmula sería: 5x-3y=46. Si “despejamos” la “x” de la primera fórmula sería: x=30-y. Ahora si sustituimos esta “x” en la segunda fórmula sería: 5·(30-y)-3y=46. Procediendo a realizar el cálculo, que sería: 150-5y-3y=46. Ahora pasamos a un lado de la igualdad (=) la incógnita (y) y al otro lado los números, cambiándole de signo (si es negativo (-) pasa a positivo (+) y viceversa). Quedando de la siguiente manera: 150-46=5y+3y, si realizamos esta operación nos da; 104=8y → y= 104:8 → y= 13 errores en total.

Silvia dibuja hormigas de la siguiente forma: una hormiga roja, otra verde, otra amarilla, otra negra, roja, verde, amarilla, negra, roja, verde, amarilla, negra…¿De qué color es la hormiga 3.452?

El resultado, es que la hormiga número 3.452 es negra. Aquí la explicación: Bueno este problema lo vamos a resolver de la forma más sencilla: Tenemos 4 colores en esta serie. Si multiplicamos cualquier número por 4 x 10= 40 y nos damos cuenta de que 40 es una hormiga negra. Otro ejemplo es 4×2 que es igual a 8, si contamos vemos claramente que el número 4 es negro, el 5 rojo, el 6 verde, el 7 es amarillo y el 8 negro. Por eso sabemos que el 3.452 es negro, porque todos los múltiplos de 4 son negros. Sabemos que son múltiplos de 4, porque al dividir da número entero sin ningún resto. En conclusión el número 3.452 es negro.

Problema 3. Desarrollado por Gloria González Fernández y Ulises Martín Melián (4º ESO-A).

Álex y Bea tienen 10 tarjetas numeradas con los números 1, 2, 3,… 10. Juegan a un juego en el que uno de ellos debe usar tres tarjetas para obtener la suma que diga su compañero. Por ejemplo, si Álex dice: 6, entonces Bea debe encontrar tres tarjetas que sumen 6. En este caso Bea tiene una única posibilidad; debería escoger necesariamente las tarjetas 1, 2, 3.

a. Bea dice: 7. ¿Qué tarjetas puede escoger Álex?

Hemos planteado el problema de la siguiente forma: Hemos visto que la única combinación posible de 3 tarjetas que sumen 7 son 1, 2 y 4.

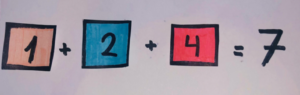
b. Quitamos cinco de las diez tarjetas y Álex dice: 8. Bea se da cuenta entonces de que puede sumar el número 8 con dos tríos distintos de tarjetas. ¿Qué tarjetas hemos quitado?

En este caso, hemos calculado primero todas las posibilidades. Han sido 1, 2, 5 y 1, 3, 4; por lo que las cartas restantes -6, 7, 8, 9 y 10- serían las que se quitan.

c. Quitamos una de las 10 tarjetas y Bea dice: 10. Álex se da cuenta entonces de que puede sumar el número 10 con un sólo trío de tarjetas. ¿Qué tarjeta hemos quitado?

Hemos seguido el mismo procedimiento previo: calcular todas las combinaciones posibles y eliminar las cartas sobrantes. En este caso, las combinaciones son las siguientes:

Por lo que las tarjetas 8, 9 y 10 son las únicas que podríamos eliminar.

d. Quitamos una tarjeta y Álex dice: 25. Bea no puede encontrar ninguna combinación de tres tarjetas para que sume 25. ¿Qué tarjeta hemos quitado?

Hemos seguido el mismo primer paso: calcular todas las combinaciones. En este caso, nos dicen que no se puede hallar 25, y el número 10 se encuentra en todas las combinaciones, por lo que es la carta que no usará Bea.

e. Quitamos una de las 10 tarjetas y Bea dice 16. Álex se da cuenta entonces que puede sumar el número 16 de 6 formas distintas. ¿Qué tarjeta hemos quitado?

Nos damos cuenta de que podemos calcular más de 6 combinaciones, por lo que se quitarían las cartas tras las cuales podríamos seguir obteniendo 6 sumas. Si quitamos el 1, 4, 8 o 10, Álex seguiría obteniendo 6 combinaciones.